It’s been about a year since the last overhaul of Synthetic Systems. Not very long in SS years … but this isn’t one. Strictly speaking anyway. The algorithm remains the same. The gears, levers, belts, pulleys, plumbing and wiring are as far as I can tell in about as good a form as they’re apt to get under my hand. But the under-the-hood changes pretty much stay under the hood, affecting only the quality of the forecasts. The stuff you see plotted on the charts has been unchanged for several years. The last change in the body work was to break a combined gold and copper plot into its individual components.
The Bond Market
In particular SS’s treatment of the US Treasury market has been focused at the two extremes of maturity, zero and infinite. There’s really no such thing as either. The underlying strategy has been for SS to treat the corners of the financial markets, leaving to the user the exercise of interpolating between them to find particular areas of interest. Want the SS forecast for silver? Look at gold and copper and read between the lines. Want junk bonds? Look at stocks and bonds and read between the lines. Read between the lines … literally.
So SS plots the extremes of the Treasury market. Want the SS forecast for medium term maturities? Read between the short and long lines. What about shorter term maturities? Read closer to the short line. Longer? Read closer to the long line.
This treatment was also partly motivated by the simpler math at the spectrum extremes. At zero maturity, there is no price change with a change in yields. At infinite maturity, price varies with the reciprocal of yield. In between, it gets more complicated.
This works well enough as long as yields don’t get too low. But as you recall from basic math, dividing by zero is verboten. Calculus offers ways to deal with such special situations, but as any denominator even gets into the zero neighborhood, the slightest perturbation results in a huge disruption of the result.
And as we said, at infinite maturity, price is reciprocal of yield. When it approaches zero, this puts yield squarely in the denominator danger zone. Price can approach infinity. As a practical matter, people don’t directly buy and sell at yields, they buy and sell at prices. Yield is the consequence of price, not the other way around. So real markets are never in danger of infinite prices based on zero yields. But bond market data are almost always quoted in terms of yield. For whatever reasons, going by most of their reporting, the financial media decided stocks just have prices and bonds just have yields.
So in order to properly take price changes into account in our total return plots, it is necessary to convert yields back into prices, and that’s where things can get dicey. In fact world markets have notoriously been through a phase where many reported yields went negative, even for some fairly long maturities. While this may seem irrational at first, it’s simply the result of the price being paid being greater than the sum of all specified cash flows – coupon and principal payments. If you believe someone else will pay an even higher price for the bond, it’s not irrational at all. The greater fool argument might be levied, but that can also apply at positive yields. Regardless, the resulting effect on SS plots is that at low yields the Bonds plot gets wild, soaring and plunging more than any real world Treasury security. Although some entities do issue infinite maturity (perpetual) bonds, Treasury does not.
This accounts for the crazy amplitude of the Bonds plot. Although site guidance explains Bills and Bonds are hypothetical zero and infinite maturity securities, the absence of anything in between may tempt readers to put more stock in them than is warranted. And between zero and infinity there’s a bit of a gap to fill. So I would like to have something more representative of real world Treasuries. The main hurdle has been formidable, messy math. A ten year treasury bond, for instance, has twenty semiannual coupon payments and one principal payment. What is the price of a bond paying a coupon of 5% of par (principal at maturity) for ten years if the prevailing market rate is 4%? You have to discount twenty one discrete cash flow data at 4% to find out. Just for one bond. For the whole market, well… We ask not because bonds routinely trade at par, but because Treasury publishes copious data on par equivalent yields. So if we want to find total return, which partly depends on price changes, we have to do some math to make use of it.
I don’t like messy math. Not very efficient either if you want to do it thousands of times to cover an array of maturities over the course of years. But I nevertheless wanted to accurately model total returns for finite maturity bonds based on readily available yield data. The solution turned out to involve a simple, elegant transformation. It is possible to translate published yield data based on multiple discrete coupon payments into an equivalent continuous cash flow, then do the price and yield calculations all in the domain of continuously compounded interest. Continuously compounded interest may be unfamiliar to many even in finance, but any regular compounding frequency, including the semiannual kind underlying the Treasury data, can be converted into this form, where the math for handing it is simple and powerful. Cumbersome metavariables like duration and convexity are implicitly accounted for without having to be directly handled.
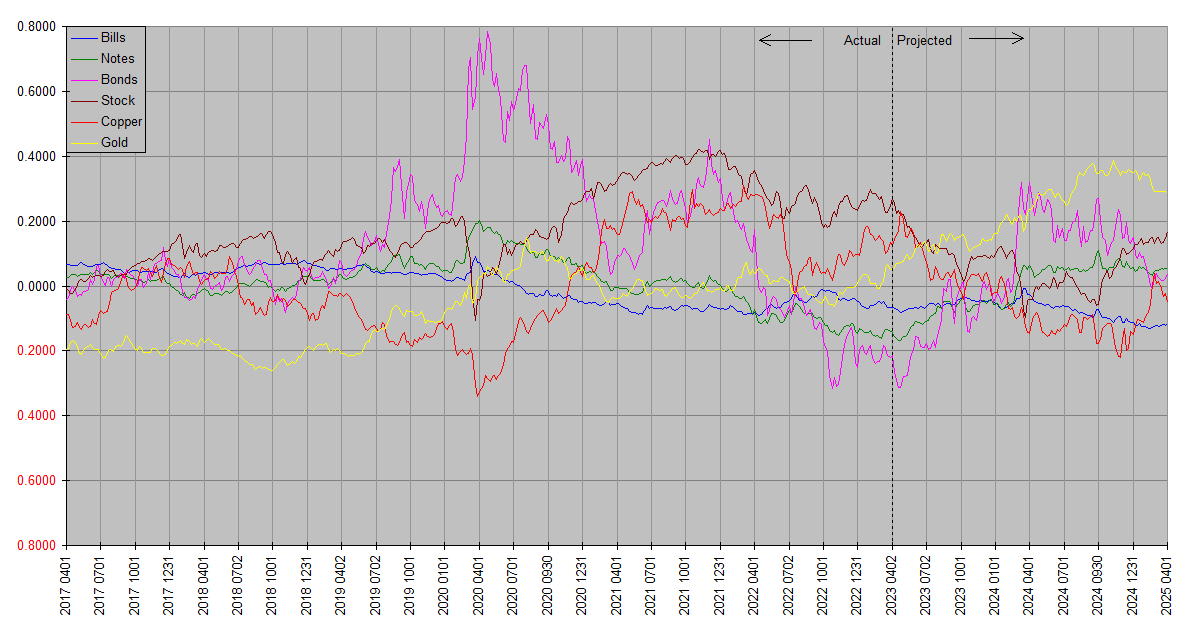
The bottom line is SS now has accurate total return data for all real world finite maturities for which Treasury publishes data. The most obvious visible result of this is in the addition of a Notes plot to the Synthetic Systems chart. The “Notes” moniker is an understatement … in fact it is the total return of the entire US Treasury market, specifically all marketable nominal securities for which yield data are published by the United States Treasury at Daily Treasury Par Yield Curve Rates.
It’s triangle weighted inversely by maturity so that shorter maturities are more heavily represented and the average weighted maturity is ten years. Although it represents the entire UST maturity spectrum, from zero to thirty years, I call it “Notes” because it happens to come pretty close to the result you would get if you just looked at the part formally referred to as “Notes”, and also because it falls between Bills and Bonds in aggregate effective maturity.
Speaking of which … the familiar Bills and Bonds plots are being kept on, with some more minor tweaking. This allows the new charts to remain comparable with the old ones. It also allows the charts to retain a visual vector indicating how maturity affects returns. The main Treasury plot is Notes, and it very closely represents the performance of the widely held iShares broad treasury fund GOVT. You still have to visually interpolate if you want to estimate a shorter or longer term fund, but it’s much less of a stretch.
I encourage bond investors to look first at the green Notes plot, then move a bit towards either Bills or Bonds lines as appropriate to visually find the maturity range of interest. Notes is the real live, real world UST market.
So what we have is a way of finding and plotting total returns of Treasuries across the spectrum, including the net result of both interest payments and price changes.
At the risk of sounding like an old late-nite infomercial though – wait … there’s more – there’s one other, lesser known source of bond returns that we’ve modeled in as well: Roll yield.
What’s roll yield? Well, the ten year bond you buy today isn’t quite a ten year bond tomorrow. It’s eventually a nine year bond, then five, etc. In general, as you hold a bond, it grows shorter in maturity. This also changes the yield, which also affects the price, and in turn total return. The same happens inside funds that own bonds. The yield curve itself owes its existence to the fact that yields differ according to maturity. Where the yield curve slope is positive (as it is most of the time over most of the curve) roll yield is positive. Where and when it’s negative, roll yield is negative.
So if we’re to accurately plot bond market total returns, we have to account for the contributions of roll yield too. And so we have. This only applies, by the way, to the comprehensive new Notes plot … there is no roll at zero and infinite maturities.
Real Returns
Another change is in the vertical axis. It has heretofore been strictly relative returns, nothing implied about the absolute, nominal or real. One plot rising or falling more than another simply indicates outperformance or underperformance. After all, the best you can do is the best you can do. Investments are sometimes dissed on the basis of losing in dollar terms or relative to inflation. But what if they’re all losing in dollar terms or to inflation? Doesn’t matter, there isn’t anything you could do about it if they were. You can only select from the assets on the menu. There is no such thing as an asset assured to outperform inflation (TIPS included).
It’s still relative returns. But nothing prevents us from scaling the vertical axis any way we find useful. Each of the plots now represents real returns. If it’s ascending, it’s gaining in real terms; if it’s descending, it’s losing in real terms. I encourage users to continue to focus on relative performance, but have used the Financology Dollar Index (FDI) methodology to put them in terms of absolute value as far as practicable. As long time readers are aware, this means units of human time, ℏ or ℍ. We’ll discuss this in more detail in an upcoming post, but in any case, the relative returns plotted are unaffected. If for instance stocks outperform gold by 5% over some time frame, that will be the case in any units you choose … in dividing the price of stocks by the price of gold, units cancel out. Literally … or rather mathematically … (A/X)/(B/X) = A/B. Graphically, this means the whole set of lines may bend up or down a bit compared to before, but the differences in their slopes (relative returns) are invariant. So it requires no change in how you read the charts; it’s just an extra in case you’re curious.
Discriminating readers may be wondering though … if Notes covers the entire Treasury market, why still have separate plots for Bills and Bonds? Why not just call Notes “Treasuries”, and leave the others out?
We could. That’s purely a matter of what you find most useful. The addition of the Notes plot does bring the total asset class plot count to six, three just for the US Treasury market. Some people might find the charts a little too busy. Others like charts that look like Christmas trees. Personally I lean towards the former, but as mentioned above the Bills and Bond plots provide a visual indication of how returns vary with length to maturity.
The same sharp-eyed readers may also notice that the other plots look a little different as well. This is a consequence of both of these changes. Giving SS more data on the Treasury market helps improve its projections, and the real return scaling affects the plots as well.
Without further ado, let’s look at a sample.
do you think it’s worth separating oil from copper?
Let me look into that, JK. There are some issues that would need to be dealt with. To start with, oil is not actually in copper now … I think we talked before about copper being representative of industrial commodities, but the Copper plot is actually just copper. The “representative” aspect is highlighted by ths chart of both. As you can see, the correlation is quite strong:
Notice that the chart ends at the beginning of 2020. It’s not even possible to properly update it beyond that, because oil prices went negative in April of that year. I noted in the above post how it’s possible to address negative yields in bondland … but negative prices just blow up the math. Everything turns to error values. Putting raw oil in SS would destroy it.
We would also have the problem of increasing the plot count to seven, making the charts less readable. A seventh plot would have to be quite different from any of the other six or the lines would come out too close, overlapping, crossing, recrossing. I actually entertained adding a separate real world short term treasury plot or dollar plot but passed on it because it was too close to the Bills plot, forcing a choice between one or the other. The same thing would happen with an oil and copper plot … it would be hard to visually separate them on an already pretty busy chart.
Ideally we would have an “Energy” plot … the price of, say, a kilojoule of energy, independent of form. Electricity, for example can be generated from anything based on its energy capacity. But I have not been able to find such data.
The next best thing might be the GSCI commodity index, the majority of which is energy commodities. There are no negative numbers in the series, and it adapts to changing industrial volumes. Assuming I can find good historical data, we could mix this in with Copper, if you think that would be if any use. The result would be further improvement in how Copper represents oil, and also have the benefit of muting some of the fluctuations due to transient issues peculiar to copper. Between the already good correlation of oil with copper and the inclusion of actual oil, you could for all intents and purposes read the Copper plot as oil. I don’t want to completely remove copper though because of its timeless and unchanging nature. Like gold, copper hasn’t changed in thirteen billion years, and the timeless constancy and presence of a fixed amount on the planet provide SS with a solid anchor. Copper didn’t suddenly become popular a mere century or so ago and it’s not vulnerable to going out of style to the extent efforts to decarbonize energy were to succeed.
So I think the realistic options are either to keep Copper copper as it is or to mix it maybe half and half with the GSCI index.
Thoughts?
tough question. the oil/copper correlation through 2020 looks impressive, but i have a hunch that oil will decouple going forward because of under-investment in capex. otoh, if you use electricity the adoption of small modular nukes might have a big impact eventually [a bunch of years out].
the negative oil price in april 2020 was a real anomaly because of limited storage capacity for wti. you could just interpolate across that period and get a better representation of prices. otoh [how many hands am i up to?] wti and bno decouple from time to time, and i can imagine geopolitical circumstances in which that decoupling might matter.
so bottom line, gsci – which contains both wti and bno – seems pretty good. however, i’m curious if it looks any less correlated with straight copper.
Yeah it is a tough call. When it comes to SS I try to avoid making subjective judgments as much as possible. Ultimately I may just have to try it and see which way works better.
Keep in mind though that SS never overrides your view of the fundamentals. If you believe oil will outperform, you invest in oil. SS then might assist in determining when the best times to take positions might be and via what asset classes.
SS is about the cyclical aspect of the financial system. It doesn’t attempt to capture or model long term fundamentals. Even if there were an explicit dedicated oil plot it probably wouldn’t have a clue as to its long term direction.
There’s a good argument for mixing in the GSCI though. You could make a case that the combo would represent copper even better than copper itself. It would reduce the impact of erratic events like the odd mine fire or flood or political disruption that adds transient noise but has nothing to do with the broad drivers of commodity prices. You could make the same case with oil … the GSCI helps smooth out the effects of isolated events like SPR manipulations or transient OPEC politics. And its composition adapts to changing market mix.
The idea of just smoothing over the negative oil prices occurred to me too. But fundamentally it’s just putting in fake data based on a judgment call … and if you’re going to do that anyway why not just use the GSCI … it smoothed out the problematic WTIC data by mixing in Brent, gas, and other other commodities. And as it turns out, that’s also pretty much what copper prices did … oil tightly tracked copper through the first half of 2020 … except for that period of a few weeks when it fell off the charts.
The high weighting of energy in the GSCI reflects its big economic footprint, so there’s no disputing the importance of oil. But for the same reasons it’s got a lot of politics in it. There’s no Strategic Copper Reserve for politicians to play with and less temptation to weaponize it for geopolitical purposes as with the sanctions on Russia.
Copper’s ten thousand year history of human use aside, its leading response to monetary changes makes it key for SS. In early 2020 it went into free fall before stocks did, leading by several weeks. You can see this in the SS charts including the one posted above. Check out 2018 too … copper led stocks down by at least a quarter. Its reputation for a PhD in economics isn’t without foundation.
Much appreciate your input, JK … I’m always on alert for ways to make SS more relevant to the people who follow it as well as more accurate.
Here are a couple charts to shed a little light on the issue.
The first one is the S&P GSCI, plotted along with WTIC (West Texas Intermediate Crude), the US oil benchmark. I’ve updated this to today, bypassing the negative price problem by restricting the data to weekly closes (though that still leaves quite a plunge into the abyss).
The next one is again the S&P GSCI, this time along with a half-and-half combo of WTIC and copper, a quick proxy for a Financology commodity index.
The main difference here is the GSCI is a little less volatile. That’s to be expected, considering it’s an index of 24 commodities. But given that my much less sophisticated index is just 2, the similarity is striking.
The latter has also slightly outperformed the GSCI over the twenty three plus years shown, primarily because oil has underperformed copper. This is also visible on the earlier 2020 chart of just copper and oil.
The correlations though must reflect something more fundamental than individual commodity factors. It’s safe to assume that an inorganic red metal and an organic black liquid aren’t colluding behind some metaphysical curtain and conspiring to jump and dive together!